Initialisation
![]()
The problem
Presumably everyone reading this uses Mathematica and also sometimes performs mathematical derivations the traditional way with pencil and paper. My aim, is to make it possible to use Mathematica as an intelligent assistant in traditional derivations – so that users can combine their insights with Mathematica\[CloseCurlyQuote]s brute force calculating strength.
Although .nb files are referred to as \[OpenCurlyQuote]notebooks\[CloseCurlyQuote], there are many steps that we might use in a real notebook, or on the back of an envelope, that can\[CloseCurlyQuote]t easily be done in Mathematica. For example, consider the following expression:
![]()
Suppose we wanted to split this into a sum of logs, we could try something like
![]()
![]()
This is all very well, but it is awfully easy to make a mistake – particularly when dealing with very complicated expressions. For example:
![]()
![]()
The problem is that when you apply a transformation rule, it is up to you whether that rule is mathematically valid.
It is also far from obvious how to extract just one specific expression – unless you are already using my ColourMaths package:
![]()
![]()
(Bear in mind that in a real problem, the various sub-expressions might be much larger than in the above.)
This paper doesn\[CloseCurlyQuote]t explain the ColourMaths package in detail, because I want to discuss the issue of using Mathematica to help perform actual derivations is a slightly larger context. However, the red colour in the above example is inserted by selecting the relevant sub-expression and using the ColourMaths palette. Colouring the text with the Mathematica menu is not the same process. Obviously I hope this discussion will encourage you to download the (free) ColourMaths package from my website.
Colouring an expression enables the selective application of a whole range of operations such as:
• Moving it out of a larger expression (as above).
• Moving it into an expression.
• Moving it to the other side of an equality in the mathematical sense.
• Making multiplicative or additive adjustments at specific locations in expressions.
Because you select the areas to be coloured, these operations enable a wide variety of operations to be specified, which would be otherwise difficult or impossible. Here is a second small example:
![]()
![]()
The Factor function is applied specifically to the red part of the expression. By comparison, when applied to the whole expression, it has no effect:
![]()
![]()
Inert operations
The ColourMaths package contains special support for derivations that involve sums, products, integrals, and limits. These are normally simply evaluated by Mathematica – one of its great strengths, of course – but you don\[CloseCurlyQuote]t always want this to happen while performing a derivation. For example, consider this sum (and evaluate it if you wish!):
![]()
There are several reasons to avoid this automatic evaluation:
• You may be performing an exercise, rather than original research, and not want Mathematica to apply its vast \[OpenCurlyQuote]knowledge to your problem, or you may be exploring alternative solutions to a known problem.
• Your expression may not be evaluable using Mathematica, but nevertheless cause Mathematica to enter a lengthy calculation, and maybe emit error messages of various sorts.
• Your expression may not yet be evaluable for technical reasons. For example, you might have an integral of this form:
![]()
![]()
Obviously the symbol F was meant to be a function of x, but this had not been made explicit.
For all these reasons, I introduced this set of four inert operations:
![]()


![]()
These inert operations are only 1-dimensional at present. Their inert nature is indicated by the background shading. Their nature is apparant if you examine them in InputForm, for example:

The ColourMaths package contains special display rules that give these constructs their appearance in StandardForm.
Let us first look at how these can be used by a student learning elementary calculus.
![]()
![]()

Note that these two steps can be combined. The red part of the expression is the part to be integrated in the integration by parts procedure.
Although the ByParts function is provided in the ColourMaths package, in general this package obviously cannot contain all the mathematical operations you might want to use. The general idea is that you supply your own operations, as we will see shortly. The crucial point, is that without the ColourMaths package, it is difficult to define integration by parts at all – because there is no way to pick out the part that is to be differentiated.
Highlight formulae
Most serious mathematical derivations number certain formulae so that these can be referred to at subsequent points in the text. While Mathematica does permit equation numbering, it supplies no way to actually access an equation by number. Although it would probably be possible to create such a mechanism, another problem associated with relying on equation numbering, is that inserting an extra numbered equation into a notebook will cause the other equation numbers to change.
The ColourMaths package lets you highlight any cell and give it a name to identify it further down the notebook. This is done by clicking anywhere in the cell, and pressing the \[OpenCurlyDoubleQuote]Highlight\[CloseCurlyDoubleQuote] button on the palette. For example:

Once this highlight formula has been named in this way, it can be refereed to thus:
![]()

Using the following extra definitions (which might typically be included in the initialisation section of a notebook), we can access the formula in a more interesting way:

![]()
![]()
• Note that assigning the physical constants to their numerical values may seem to be a more obvious approach, but using assignments to variables that may appear in expressions is almost always a bad idea. For example, once assignments had been made,it would mean that the above formula would be unobtainable in its symbolic form without clearing all the relevant variables.
• Note also that with Mathematica version 9 or above, it would make sense to use Quantity objects inside physicalConstants definition.
• Get\[Breve]Highlight\[Breve]Formula extracts the formula from the currently selected notebook, or from a specified notebook supplied as a second argument. It does not use the current contents of the kernel except that the ColourMaths package must be loaded.
• If you prefer to number your equations, you can always give them a numerical name, e.g. \[OpenCurlyDoubleQuote]23\[CloseCurlyDoubleQuote] or \[OpenCurlyDoubleQuote](23)\[CloseCurlyDoubleQuote] or \[OpenCurlyDoubleQuote]2.1.7\[CloseCurlyDoubleQuote] .
Point and click transformations
Perhaps the most powerful way to transform an expression, is to select all or part of an expression, and press the \[OpenCurlyDoubleQuote]Adjust button to display a menu of possible transformations of the selection. This menu is constructed out of certain built-in transformations, plus ones that you define yourself.
Since the whole idea of ColourMaths is to leave you with a set of executable steps covering all or most a mathematical argument, the adjustment is performed in a way that allows it to be repeated without accessing the menu again. While this mechanism does contain some built-in transformations, it is most powerful when used with user-supplied transformations:

• Important note: The above theorem has conditions on | x | for certain values of p. The ColourMaths package is concerned with the mechanical steps in a proof, checks for convergence etc should be inserted to augment the proof, but these are typically best added later, after the sequence of required steps has been established.
Here I have used a gray colouration to represent selection in the usual Mathematica fashion.
![]()
![]()

• In the above, the variable k is coloured magenta using the \[OpenCurlyQuote]Flag\[CloseCurlyQuote] colour from the palette. This signifies that it is a dummy name – to be replaced by the user. This is important when, as here, a transformation introduces a construct such as a sum that contains a dummy variable. As you will see below, it can also be used to insert constants or even expressions.
• In general, it is suggested that a notebook containing a mathematical derivation should start with an initialisation section that loads the ColourMaths package, and supplies a number of Define\[Breve]Adjustment calls to provide various high level transformations.
Performing numerical checks
One of the great features of Mathematica, is that it is often easy to do numerical checks of formulae as you develop them. These are best set up with suitable values as required for a particular derivation, and are often best performed on equalities. Not that because numerical comparisons are rarely exact, the equality head is replaced by an inert head for the purposes of display.
Numerical summations and integrations can go wrong if they operate on something that still contains variables. It is therefore best to prepare the numerical version of the equality inside of Hold, and then release it at the end.
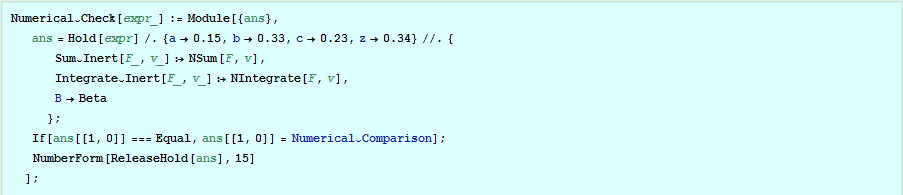
It can take a little effort to devise a good Numerical\[Breve]Check routine, but if your derivation is at all complicated, it is definitely worthwhile. I am yet to think of a satisfactory way to automate this process.
In order for arbitrary numerical substitutions to work, it is, of course necessary to take into account any convergence criteria. These can be calculated, or obtained by Mathematica – for example:
![]()

If the convergence criteria are not clear, it is worth experimenting a bit with the numbers used because numerical checks are very useful. It is also best to use non-integer values for variables that are meant to be real because integer values might hit special cases of one kind or another.
Numerical checks are not possible for certain types of calculations, particularly physics derivations,that might contain some undefined functions – unless perhaps you supplied an approximate form for such a function.
Example 1
It is only as we get to more complex examples that we can really see the scope of the ColourMaths package.
We wish to show the following identity, where B (capital \[Beta]) represents the Beta function.

As you read it, remember that the output from one step becomes the input to the next – often with the addition of some colour. Sometimes this colour is put in explicitly with one of the colour buttons, sometimes it is put in implicitly by highlighting an expression and performing an Adjust operation. In some cases, for clarity, I have duplicated the output from one step before manipulating it further.
Let us start by doing a numerical check on what we want to prove – it is so easy to drop a sign in the very expression you are trying to prove!
![]()
![]()
As you can see, the comparison is not exact because both the sum and the integral are computed to finite precision.
We need the binomial theorem, as above.

Here is a suitable definition of the beta function

Now we pick up the LHS of the expression to be proved, highlight the term (1-t , press the Adjust button, and select the binomial expansion.
![]()
![]()
SwapOperations swaps the sum and integral. Although it does ensure that the inner dummy variable (j in this case) is not present in the larger scope, it doesn\[CloseCurlyQuote]t perform the necessary convergence checks. These should be added afterwards if desired.


This step splits the t z factor and moves the Binomial outside the integral.
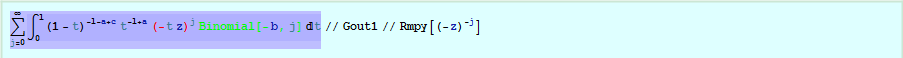
Since j is obviously an integer, it is valid to use PowerExpand to simplify the Red expression

Now we move the term in z outside the sum, by first colouring it red.


Finally, we select the integral, use the Adjust button, and pick the transformation to the beta function.


• Typically you might want to either place the Define\[Breve]Adjustment and related calls in an initialisation section at the start of your notebook, or if you anticipate performing a number of related derivations in different notebooks, even move them into a package of your own. This also has the advantage that you always use the same version of your adjustments – so if there are problems you are more likely to spot them and eliminate them!
EllipsisForm
When performing hand calculations, it is often useful to display products and sums by displaying a few typical terms. The ColourMaths package contains a function that expands inert sums and products in exactly this way. A few examples illustrate its use:



![]()


I find this representation often helps me to understand just what one of these formulae mean and how they might be manipulated – as will be seen in the next example.
Example 2
This is an example from the somewhat exotic theory of q-functions. We want to start with Identity_1 and prove Identity_2. This is one step in the derivation of Jacobi\[CloseCurlyQuote]s Triple Product.


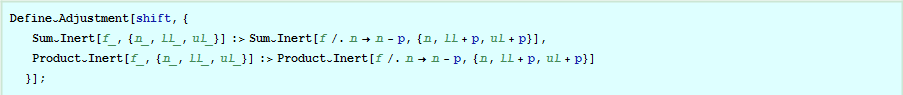
First we define a new Numerical\[Breve]Check function that treats finite sums and products differently from those with infinite limits
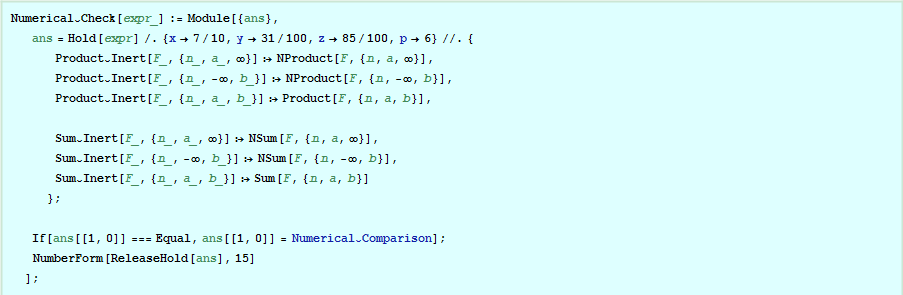
Now we can perform a numerical check on both identities
![]()
![]()
![]()
![]()
First we change indices and replace z by z/x. We can simplify the result using PowerExpand since it is only going to operate on an integer index expression
![]()


![]()
The next step is performed by selecting the LHS and using the Adjust button. It shifts the indexing of the LHS up by 1.



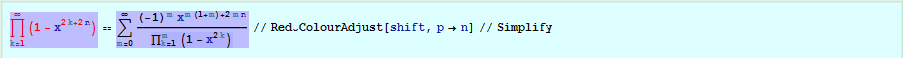


Q.E.D.
Since these formulae are rather messy, it is worth letting Mathematica check for symbolic identity.

![]()
Final comments
• This is obviously an open-ended project, and has focused on one particular area of mathematics, that seems to me to be particularly well suited to the ColourMaths package. It shows just how much formula manipulation can be controlled by Mathematica.
• I think the use of highlight formulae binds derivations together because it permits explicit access to earlier results without requiring that the notebook is evaluated in order. This mimics the way people use actual paper notebooks.
• The use of the Adjust button alleviates a lot of the burden to figure out exactly which transformations does what.


